対数クォータニオンノード（Maya2016）

Maya pythonの練習として，対数クォータニオンを扱うノードを作成してみました．具体的には，オイラー角と対数クォータニオンとを相互に変換する2つのユーティリティノード mlEulerToExpmap と mlExpmapToEuler を作成しました．

本記事では，クォータニオンやクォータニオンの対数の理論は脇に置き，pythonによる実装コードのみ解説します．対数クォータニオンの解説については，CEDECでの拙発表資料などをご参照下さい．今回の開発環境は Maya2016 + Maya Python API 2.0です．ソースコードは下記のGitHubリポジトリからご利用下さい．

https://github.com/mukailab/maya

1. mlEulerToExpmapノード

1.1 概要

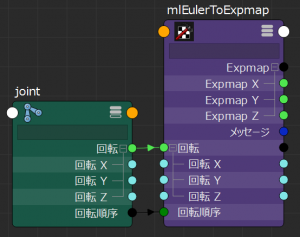
mlEulerToExpmapノードはオイラー角を入力アトリビュートに持ちます．これは，標準的なMayaのノードでは「回転」と記述される，X軸周り回転角，Y軸周り回転角，Z軸周り回転角の3つ組の角度データです．また，オイラー角利用の際に指定すべき，X軸，Y軸，Z軸の「回転順序」も入力アトリビュートとして持ちます．これらの入力アトリビュートをもとに，オイラー角に対応する対数クォータニオン「Expmap」を計算して出力します．対数クォータニオンも(X，Y，Z)の3つ組の値です．

ここで，クォータニオンを\({\bf q}=[q_x, q_y, q_z, q_w]\)とするとき，対数クォータニオン\({\bf e}=[e_x, e_y, e_z]\)は次式で計算されます．

\(
{\bf e} = \ln({\bf q}) = \left[q_x \frac{\theta}{\sin(\theta)}, q_y \frac{\theta}{\sin(\theta)}, q_z \frac{\theta}{\sin(\theta)}\right] \\
\theta = \cos^{-1}(q_w)
\)

以降，mlEulerToExpmapノードの実装コードを示します．

1.2 モジュール変数

まず，ファイル冒頭で各入出力アトリビュートのロングネームとショートネーム，ナイスネームを定義しておきます．API 2.0 を利用するためのおまじないメソッドも加えています．

# -*- coding: utf-8 -*
import math
import maya.api.OpenMaya as OpenMaya

nodeName = 'mlEulerToExpmap'
expmapName = ('expmap', 'em', u'expmap')
expmapElementName = (('expmapX', 'emx', 'Expmap X'),
                     ('expmapY', 'emy', 'Expmap Y'),
                     ('expmapZ', 'emz', 'Expmap Z'))
rotateName  = ('Rotate', 'ir', u'回転')
eulerAngleName  = (('rotateX', 'rx', u'回転 X'),
                   ('rotateY', 'ry', u'回転 Y'),
                   ('rotateZ', 'rz', u'回転 Z'))
rotateOrderName  = ('rotateOrder', 'ro', u'回転順序')

def maya_useNewAPI():
    pass

# -*- coding: utf-8 -*

import math

import maya.api.OpenMaya as OpenMaya

nodeName = 'mlEulerToExpmap'

expmapName = ('expmap', 'em', u'expmap')

expmapElementName = (('expmapX', 'emx', 'Expmap X'),

('expmapY', 'emy', 'Expmap Y'),

('expmapZ', 'emz', 'Expmap Z'))

rotateName = ('Rotate', 'ir', u'回転')

eulerAngleName = (('rotateX', 'rx', u'回転 X'),

('rotateY', 'ry', u'回転 Y'),

('rotateZ', 'rz', u'回転 Z'))

rotateOrderName = ('rotateOrder', 'ro', u'回転順序')

def maya_useNewAPI():

pass

1.3 クラス定義の冒頭

クラス定義の冒頭部分のみ示します．メンバ変数宣言に続き，__init__メソッドと，インスタンス生成を行うcreatorメソッドを示します．

class mlEulerToExpmap(OpenMaya.MPxNode):
    """euler to expmap"""    
    rotate = OpenMaya.MObject()
    eulerAngles = []
    expmap = OpenMaya.MObject()
    expmapElement = []
    
    def __init__(self):
        OpenMaya.MPxNode.__init__(self)

    @staticmethod
    def creator():
        return mlEulerToExpmap()

class mlEulerToExpmap(OpenMaya.MPxNode):

"""euler to expmap"""

rotate = OpenMaya.MObject()

eulerAngles = []

expmap = OpenMaya.MObject()

expmapElement = []

def __init__(self):

OpenMaya.MPxNode.__init__(self)

@staticmethod

def creator():

return mlEulerToExpmap()

mlExpmapToEulerクラスは入出力アトリビュートに対応する5つのメンバ変数を持ちます．具体的には，rotateとeulerAnglesの2つがオイラー角を，rotateOrderがオイラー角の回転順序を，残るexpmapとexpmapElementの2つが対数クォータニオンを表します．素直に考えれば，オイラー角も対数クォータニオンもそれぞれ1つの変数で表すべきでしょうが，ここでは3つ組全体を表す変数と，各要素に対応するリストを組み合わせています．この理由については，次のinitializeメソッドの説明で示します．

1.4 ノード初期化メソッド

続いて，ノードを初期化するinitializeメソッドを示します．このメソッドは，入出力アトリビュートおよびポートの状態を設定します．

@staticmethod
def initialize():
    # output expmap
    cAttr = OpenMaya.MFnCompoundAttribute()
    mlEulerToExpmap.expmap = cAttr.create(expmapName[0], expmapName[1])
    cAttr.setNiceNameOverride(expmapName[2])
    mlEulerToExpmap.expmapElement = []
    for i in xrange(0, 3):
        nAttr = OpenMaya.MFnNumericAttribute()
        mlEulerToExpmap.expmapElement = mlEulerToExpmap.expmapElement + \
            [nAttr.create(expmapElementName[i][0],
                            expmapElementName[i][1],
                            OpenMaya.MFnNumericData.kDouble,
                            0.0)]
        nAttr.setNiceNameOverride(expmapElementName[i][2])
        nAttr.keyable = False
        nAttr.writable = False
        cAttr.addChild(mlEulerToExpmap.expmapElement[i])
    mlEulerToExpmap.addAttribute(mlEulerToExpmap.expmap)
        
    # input Euler angles
    cAttr = OpenMaya.MFnCompoundAttribute()
    mlEulerToExpmap.rotate = cAttr.create(rotateName[0], rotateName[1])
    cAttr.setNiceNameOverride(rotateName[2])
    mlEulerToExpmap.eulerAngles = []
    for i in xrange(0, 3):
        uAttr = OpenMaya.MFnUnitAttribute()
        mlEulerToExpmap.eulerAngles = mlEulerToExpmap.eulerAngles + \
            [uAttr.create(eulerAngleName[i][0],
                            eulerAngleName[i][1],
                            OpenMaya.MFnUnitAttribute.kAngle,
                            0.0)]
        uAttr.setNiceNameOverride(eulerAngleName[i][2])
        uAttr.keyable = True
        uAttr.readable = False
        cAttr.addChild(mlEulerToExpmap.eulerAngles[i])
    mlEulerToExpmap.addAttribute(mlEulerToExpmap.rotate)
    mlEulerToExpmap.attributeAffects(mlEulerToExpmap.rotate, mlEulerToExpmap.expmap)

    # input rotation order
    nAttr = OpenMaya.MFnNumericAttribute()
    mlEulerToExpmap.rotateOrder = nAttr.create(rotateOrderName[0],
                                                rotateOrderName[1],
                                                OpenMaya.MFnNumericData.kInt,
                                                0)
    nAttr.setNiceNameOverride(rotateOrderName[2])
    nAttr.readable = False
    mlEulerToExpmap.addAttribute(mlEulerToExpmap.rotateOrder)
    mlEulerToExpmap.attributeAffects(mlEulerToExpmap.rotateOrder, mlEulerToExpmap.expmap)

@staticmethod

def initialize():

# output expmap

cAttr = OpenMaya.MFnCompoundAttribute()

mlEulerToExpmap.expmap = cAttr.create(expmapName[0], expmapName[1])

cAttr.setNiceNameOverride(expmapName[2])

mlEulerToExpmap.expmapElement = []

for i in xrange(0, 3):

nAttr = OpenMaya.MFnNumericAttribute()

mlEulerToExpmap.expmapElement = mlEulerToExpmap.expmapElement + \

[nAttr.create(expmapElementName[i][0],

expmapElementName[i][1],

OpenMaya.MFnNumericData.kDouble,

0.0)]

nAttr.setNiceNameOverride(expmapElementName[i][2])

nAttr.keyable = False

nAttr.writable = False

cAttr.addChild(mlEulerToExpmap.expmapElement[i])

mlEulerToExpmap.addAttribute(mlEulerToExpmap.expmap)

# input Euler angles

cAttr = OpenMaya.MFnCompoundAttribute()

mlEulerToExpmap.rotate = cAttr.create(rotateName[0], rotateName[1])

cAttr.setNiceNameOverride(rotateName[2])

mlEulerToExpmap.eulerAngles = []

for i in xrange(0, 3):

uAttr = OpenMaya.MFnUnitAttribute()

mlEulerToExpmap.eulerAngles = mlEulerToExpmap.eulerAngles + \

[uAttr.create(eulerAngleName[i][0],

eulerAngleName[i][1],

OpenMaya.MFnUnitAttribute.kAngle,

0.0)]

uAttr.setNiceNameOverride(eulerAngleName[i][2])

uAttr.keyable = True

uAttr.readable = False

cAttr.addChild(mlEulerToExpmap.eulerAngles[i])

mlEulerToExpmap.addAttribute(mlEulerToExpmap.rotate)

mlEulerToExpmap.attributeAffects(mlEulerToExpmap.rotate, mlEulerToExpmap.expmap)

# input rotation order

nAttr = OpenMaya.MFnNumericAttribute()

mlEulerToExpmap.rotateOrder = nAttr.create(rotateOrderName[0],

rotateOrderName[1],

OpenMaya.MFnNumericData.kInt,

nAttr.setNiceNameOverride(rotateOrderName[2])

nAttr.readable = False

mlEulerToExpmap.addAttribute(mlEulerToExpmap.rotateOrder)

mlEulerToExpmap.attributeAffects(mlEulerToExpmap.rotateOrder, mlEulerToExpmap.expmap)

まず，出力アトリビュートである対数クォータニオンを設定します．対数クォータニオンはMFnNumericAttributeのk3Doubleを用いても良かったのですが，表示名が「Expmap 0」のように数字になる点に違和感があったので，複合アトリビュートMFnCompoundAttributeを用いて実装しました．親アトリビュートはexpmap（表示名「Expmap」）とし，子アトリビュートには対数クォータニオンの3要素のリスト（それぞれ表示名は「Expmap X」，「Expmap Y」，「Expmap Z」）を指定しました．このように，同一データを2つの変数で表すという冗長な構成になってしまいますが，今回はUIを優先しました．

入力アトリビュートとしては，まずオイラー角を設定します．当初は，オイラー角を扱うためにMayaの標準的な「回転」アトリビュートを使いたかったのですが，リファレンスマニュアルやweb検索でも，対応するMFnAttribute派生クラスが見当たりませんでした．仕方ないので，出力アトリビュートと同様にMFnCompoundAttributeを用いることにしました．親アトリビュートはrotation（表示名「回転」）とし，子アトリビュートにはMFnUnitAttribute.kAngleのリストeulerAngles（それぞれ表示名は「回転 X」，「回転 Y」，「回転 Z」）を指定しました．さらに，オイラー角の回転順序を表すアトリビュートrotateOrder（表示名「回転順序」）も，MFnNumericAttribute.kIntとして追加しています．

1.5 出力アトリビュートの計算

計算本体であるcomputeメソッドでは，入力アトリビュートであるオイラー角を対数クォータニオンに変換し，出力アトリビュートの値を決定します．

def compute(self, plug, dataBlock):
    if plug is not self.expmap and plug not in self.expmapElement:
        return

    r = [0, 0, 0]
    for i in xrange(0, 3):
        rHandle = dataBlock.inputValue(mlEulerToExpmap.eulerAngles[i])
        r[i] = rHandle.asDouble()
    roHandle = dataBlock.inputValue(mlEulerToExpmap.rotateOrder)
    rotateOrder = roHandle.asInt()
    eulerRotation = OpenMaya.MEulerRotation(r[0], r[1], r[2], rotateOrder)
    q = eulerRotation.asQuaternion()
    if q.w > 1.0 - 1.0e-6:
        a = 0.0
        isina = 0.0
    else:
        a = math.acos(q.w)
        isina = a / math.sin(a)
    ln = (q.x * isina, q.y * isina, q.z * isina)
    for i in xrange(0, 3):
        outputHandle = dataBlock.outputValue(mlEulerToExpmap.expmapElement[i])
        outputHandle.setDouble(ln[i])
    dataBlock.setClean(plug)

def compute(self, plug, dataBlock):

if plug is not self.expmap and plug not in self.expmapElement:

return

r = [0, 0, 0]

for i in xrange(0, 3):

rHandle = dataBlock.inputValue(mlEulerToExpmap.eulerAngles[i])

r[i] = rHandle.asDouble()

roHandle = dataBlock.inputValue(mlEulerToExpmap.rotateOrder)

rotateOrder = roHandle.asInt()

eulerRotation = OpenMaya.MEulerRotation(r[0], r[1], r[2], rotateOrder)

q = eulerRotation.asQuaternion()

if q.w > 1.0 - 1.0e-6:

a = 0.0

isina = 0.0

else:

a = math.acos(q.w)

isina = a / math.sin(a)

ln = (q.x * isina, q.y * isina, q.z * isina)

for i in xrange(0, 3):

outputHandle = dataBlock.outputValue(mlEulerToExpmap.expmapElement[i])

outputHandle.setDouble(ln[i])

dataBlock.setClean(plug)

クォータニオンの対数の計算式を素直に実装していますが，二点だけ補足します．

符号だけが異なる2つのクォータニオン\({\bf q}\)と\(-{\bf q}\)は，同一の回転を表します．しかしながら，これら2つのクォータニオンの対数は異なる値になります．しかし，これは直感に反しますので，12~13行目では，クォータニオンのw成分\(q_w\)が必ず非負となるような符号反転の前処理を行います．
\(q_w\)の値が0に近づくと，19行目でゼロ除算が発生してしまいます．こうしたゼロ除算を回避するために，14~19行目に示すように，\(q_w\)の絶対値に応じた条件判定を行います．

2. mlExpmapToEuler

対数クォータニオンをオイラー角に変換します．まず，対数クォータニオンからクォータニオンに変換し，さらにオイラー角に変換するという手順をとります．対数クォータニオンからクォータニオンへの逆変換は次式で表されます．

\(
{\bf q} = \exp({\bf e}) = \left[ e_x \frac{\sin(\theta)}{\theta}, e_y \frac{\sin(\theta)}{\theta}, e_z \frac{\sin(\theta)}{\theta}, \cos(\theta) \right] \\
\theta = \| {\bf e} \|
\)

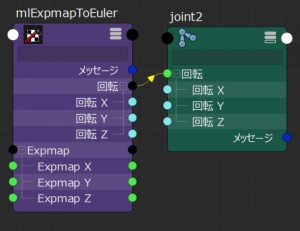
入力された対数クォータニオンを，同時に入力される回転順序にしたがってオイラー角に変換します．モジュール変数やクラス定義の冒頭，およびinitializeメソッドの実装についての解説は冗長なので省き，ここではcomputeメソッドについてのみ触れます．

def compute(self, plug, dataBlock):
    if plug is not self.rotate and plug not in self.eulerAngles:
        return

    rv = [0.0, 0.0, 0.0]
    for i in xrange(0, 3):
        inputHandle = dataBlock.inputValue(mlExpmapToEuler.expmapElement[i])
        rv[i] = inputHandle.asDouble()
    orderHandle = dataBlock.inputValue(mlExpmapToEuler.rotateOrder)
    exHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[0])
    eyHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[1])
    ezHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[2])
    mag = math.sqrt(rv[0] * rv[0] + rv[1] * rv[1] + rv[2] * rv[2])
    if math.fabs(mag) < 1.0e-6:
        sina = 0
    else:
        sina = math.sin(mag) / mag
    quat = OpenMaya.MQuaternion(rv[0] * sina,
                                rv[1] * sina,
                                rv[2] * sina,
                                math.cos(mag))
    order = orderHandle.asInt()
    euler = OpenMaya.MEulerRotation(0, 0, 0, order)
    euler *= quat
    exHandle.setDouble(euler.x)
    eyHandle.setDouble(euler.y)
    ezHandle.setDouble(euler.z)
    dataBlock.setClean(plug)

def compute(self, plug, dataBlock):

if plug is not self.rotate and plug not in self.eulerAngles:

return

rv = [0.0, 0.0, 0.0]

for i in xrange(0, 3):

inputHandle = dataBlock.inputValue(mlExpmapToEuler.expmapElement[i])

rv[i] = inputHandle.asDouble()

orderHandle = dataBlock.inputValue(mlExpmapToEuler.rotateOrder)

exHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[0])

eyHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[1])

ezHandle = dataBlock.outputValue(mlExpmapToEuler.eulerAngles[2])

mag = math.sqrt(rv[0] * rv[0] + rv[1] * rv[1] + rv[2] * rv[2])

if math.fabs(mag) < 1.0e-6:

sina = 0

else:

sina = math.sin(mag) / mag

quat = OpenMaya.MQuaternion(rv[0] * sina,

rv[1] * sina,

rv[2] * sina,

math.cos(mag))

order = orderHandle.asInt()

euler = OpenMaya.MEulerRotation(0, 0, 0, order)

euler *= quat

exHandle.setDouble(euler.x)

eyHandle.setDouble(euler.y)

ezHandle.setDouble(euler.z)

dataBlock.setClean(plug)

ここでもゼロ除算が発生しうる計算がありますので，対数クォータニオンの2-ノルム\(\|{\bf e}\|\)の値に応じて，13~16行目の条件分岐を行います．そして，21~22行目でクォータニオンからオイラー角へ変換していますが，正直書くと，これで正しいコーディングという確信がありません．実験的には正しい結果を与えているようですが，1行でスッキリと書く方法がありそうな気がしています．

3. 実験

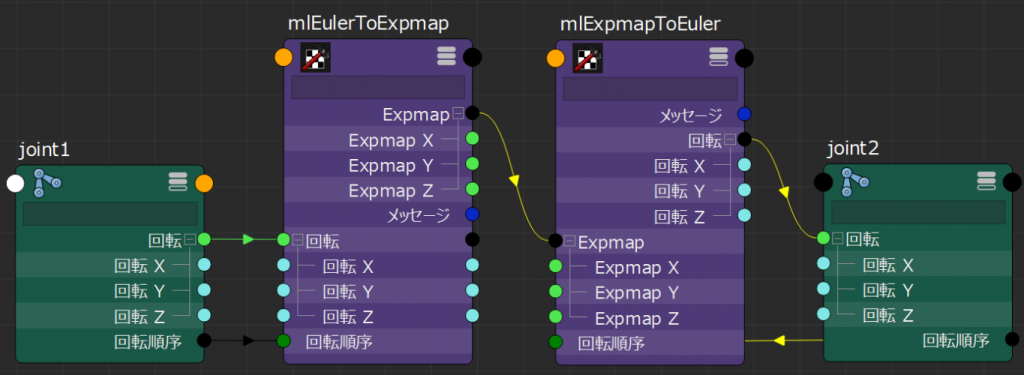
適当なjointノードの回転アトリビュートをmlEulerToExpmap→mlExpmapToEuler→別のjointの回転アトリビュートに接続し，入力と出力で同一のオイラー角が得られるか試しました．以下に実験の様子を収めたムービーを示します．

スクリーンキャプチャーのフレームレートが低く，またマウスカーソルが位置ズレしているので見づらいかと思いますが，おおむね問題なく動作している様子は伝わるかと思います．ムービー最後ではオイラー角を数値で確認していますが，2つのjointで異なる値となっています，これは，ある3次元回転を表すオイラー角は無数に存在するためです．オイラー角ではなくクォータニオンの値を確認すると，入出力が一致することが確認できるはずです．

4. まとめと課題

本記事で説明したユーティリティノードは，特殊な用途でもない限り使い道は無いと思います．ただ，直近で公開予定の補助骨プラグイン含め，本研究室から発信する情報では対数クォータニオンを扱う可能性が高いため，今回はそのコードも含めて解説してみました．

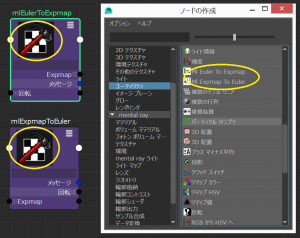
今回はMaya Pythonの練習として，リファレンスマニュアルと格闘しながら試行錯誤的にプログラミングしましたが，下図の黄色円に示すように，ノードのアイコンの設定方法が分からずじまいでした．また，「ノードの作成」におけるノード名の変更方法も分かりませんでした．解決したい気持ちはありますが，時間が惜しいのでギブアップです．